
連載一覧
連載2回目の今回はいよいよニューラルネットの基本的な概念について解説していきます。
ニューロン (neuron)
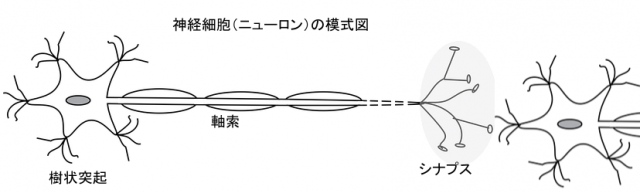
脳や神経系を形作っているのが ニューロン (neuron) と言われる細胞です。樹状突起から入ってきた電気信号の合計がしきい値以上になると神経細胞の電位が突発的に高くなります。この現象を 発火 といい、発火した電気信号は軸索と末端のシナプスを通して他の神経細胞へ連鎖していきます。シナプスでの結合は使われることで強化され、また神経細胞間の接続も増えるなど変化していきます。
形式ニューロン (formal neuron)
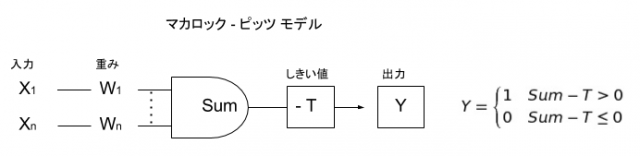
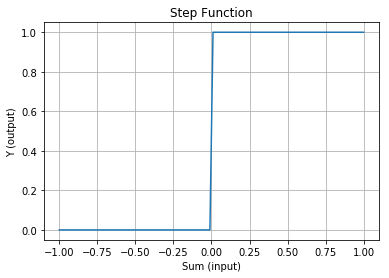
生物のニューロンを参考に数学的にモデル化したものを形式ニューロンと言います。形式ニューロンのひとつで1943年にマカロックとピッツが発表したのがマカロック-ピッツ モデルです。入力 X に重みを掛け合わせた合計がしきい値 T を越えた場合に出力 Y が 1 に「発火」するというものです。入力を出力に変換する動作は関数で表現されていて、 活性化関数 といいます。マカロック-ピッツ モデルで使われている活性化関数はグラフ化すると下図のように階段状になっているため ステップ関数 と言います。
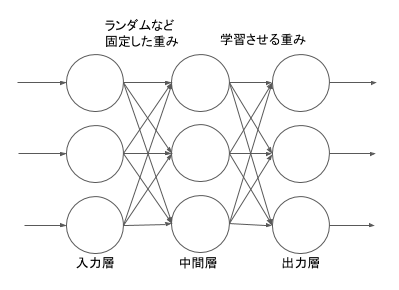
パーセプトロン (perceptron)
1958年に発表されたパーセプトロンは入力層と、ランダムで固定した結合重みを持つ大量の中間層と、重みを学習させる出力層の3層で構成されていました。パターン認識で実用的に使うには 入力層 (n 個) → 中間層 (2 の n 乗個) は当時の計算能力では使うのが難しかったため、それらを省略したものが単純パーセプトロンとも言われて応用や研究で盛んに使われていました。
単純パーセプトロンは形式ニューロンと同じくニューロン1個のモデルですが、しきい値をマイナスの値をとり得る バイアス値 として加算するように変形し、以下の式で記述できます。
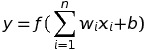
活性化関数 f には当初はステップ関数を用い、重み w とバイアス b を調整する学習の方法としては、出力した値と正解との差を使って重みを増減していくという 誤り訂正学習 を使っていました。
線形回帰 (linear regression)
統計的な機械学習の手法の一つで、ベクトルで表された観測データを結果となる実数に写像するとともに、この写像自体を何らかの評価関数を最適化して求めることを 回帰 (regression) といいます。
観測データをベクトル x、 データの重みをベクトル w とし、ベクトルの内積によって回帰の結果 y を求めるモデルを 線形回帰 (linear regression) と言い以下の式で記述できます。
観測データの先頭に疑似データとして 1 を、重みとしてバイアス値 b とすると線形回帰とニューラルネットの基本的な形態である単純パーセプトロンが同じ式になり、同一のものだということがわかります。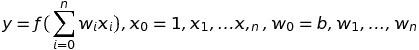
ロジスティック回帰 (logistic regression)
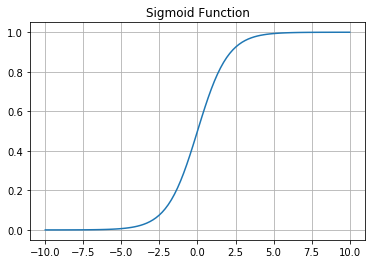
しきい値で発火する、しないというアイデアをストレートに表現したのがステップ関数でしたが、統計的・確率的に取り扱うには微分可能である方が望ましいため、代わって使われるようになった活性化関数が シグモイド (sigmoid) 関数 です。
シグモイド関数は人口統計のグラフなどで出てくるロジスティック曲線を描くロジスティック関数の一種なため、シグモイド関数を活性化関数に用いる線形回帰が ロジスティック回帰 と呼ばれます。線形回帰と単純パーセプトロンは等価なため、単純パーセプトロンでも同じようにシグモイド関数を活性化関数に使うことが出来ます。
損失関数と最適化手法
現在のシナプス、あるいはデータの 重み で計算した出力が、どれくらい正解から離れているのか、その離れ具合を関数にしたものが 損失関数、誤差関数 と言われるものです。
どんな入力が来ても損失関数を最小化してくれるパラメータ (重み、バイアス)を見つけることを 最適化 と言い、最適化でたどりついた解を 最適解 と言います。重みパラメーターを決定するという意味では最適化と学習は同じものになります。
活性化関数にシグモイド関数を使っている場合によく使われている損失関数が 交差エントロピー (cross entropy) 誤差関数です。 2値に出力する場合の損失を binary cross entroy 多値に分類する場合の損失を category cross entropy と言います。
損失関数を二次関数のように描いた場合グラフの底のように最小になるところが最適解ですすが、この最適解に辿り着くために損失関数の微分である勾配をたよりに確率的にデータを抜き出してパラメータを探索していくのが 確率的勾配降下法 (Stocastic Gradient Descent, SGD) です。
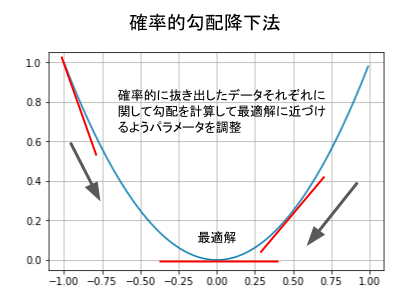
1回の学習でどれくらいの変化をパラメータに加えるかというのが、学習率 と呼ばれます。学習率が低いと学習までに時間がかかりすぎ、また学習率を高くすると1回の学習で最適解を大きく飛び越すような挙動になり解に辿り着けなくなる可能性もあるため、学習率も重要な値になります。
また、1点のデータ毎に勾配計算してパラメータを調整していくと計算時間がかかる場合がありますので、ある程度のデータをまとめて抜き出してまとめて1回の学習として勾配計算やパラメーター変更を行う方法を ミニバッチ と言います。
ハイパーパラメーター (hyperparameter)
使われているニューラルネットの基本的な理論は同じでも、以下のようなパラメーターをどうするかによって、生成されるモデル、つまり求められるニューロンの結合重みやバイアスといった学習結果が大きく変わり、ニューラルネットワークの性能自体も異なってきます。
- ネットワークの構成
- 現実のデータを、入力データや出力データとして表現する方法(実数で?二値の信号で?)
- 活性化関数
- 損失関数
- 最適化手法
- 学習率
- ミニバッチのサイズ
- どれくらい繰り返し学習させるか (epoch といいます)
これら「パラメーターを決定することになるパラメーター」のことを ハイパーパラメーター (hyperparameter) と言い、Keras はこれらハイパーパラメーターを記述・設定することにより、簡単にニューラルネットワークを使うことが出来るライブラリです。
Keras の単純パーセプトロンで OR 回路を学習してみる
ニューラルネットの基本の解説の次は、早速 Keras を使ってみます。単純パーセプトロン(ロジスティック回帰)を使って OR 回路を学習してみます。
ハイパーパラメーター
- 入力は {0,1} の信号が2つ、出力は {0,1} の信号が一つ
- ニューラルネットワーク: 一層(出力が1個なので素子数は1個)
- 活性化関数: シグモイド
- 損失関数: binary cross entropy
- 最適化手法: 確率的勾配降下法
- 学習率: 0.1
- ミニバッチ: 1
- epoch: 30
モデル構築
まず最初に jupyter-notebook のノートブック上で必要なモジュール類を読み込みます。
import numpy as np from keras.models import Sequential from keras.layers import Dense, Activation from keras.optimizers import SGD
テストに再現性を持たせるために numpy の乱数の種を任意の数(この場合 0)に設定しておきます。
np.random.seed(0)
単純に入力から出力へと多数の層になったニューラルネットワークを重ねて構成するのを Seaquential モデルと言います。今回は一層だけのネットワークですが Seaquential モデルを使います。
model = Sequential()
作成した Sequential モデルに、属性としてハイパーパラメーターを追加していきます。
入力から出力まで、上流と下流のニューロンに対してもれなく結合しているモデルを全結合、Dense と言います。 入力をベクトルとして扱っていますので、入力の個数はベクトルの次元と言われます。 OR 回路は 0 または 1 が2つ入ってきますので入力の次元数は 2 になります。 ニューロンから出る信号の経路は一つだけとし、同時に複数の出力を出す必要がある場合はその分のニューロンを用意します。 今回は 0 または 1 を表現する出力が1個あればよいので、この層あたりのニューロンは1個になります。
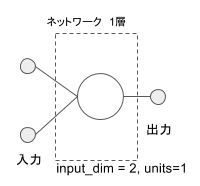
入力次元が 2 で、出力ユニット数が 1 の全結合の属性を追加します。
model.add(Dense(input_dim=2, units=1))
この層は活性化関数としてシグモイド関数を使います
model.add(Activation('sigmoid'))
binary cross entropy の損失関数に対して確率的勾配降下法 (SGD) を用いて、学習率 (learning rate) 0.1 で学習を行うモデルにします。
モデルの設定は以上になりますので最後にモデルをコンパイルして生成します。
model.compile(loss='binary_crossentropy', optimizer=SGD(lr=0.1))
以上で単純パーセプトロンのモデルが構築できました。
訓練データ準備
OR 回路の入力データ X を4行2列の numpy の配列で、正解データ T を4行1列で準備します。
X = np.array( [[0,0],
[0,1],
[1,0],
[1,1]] )
T = np.array( [[0],
[1],
[1],
[1]] )
トレーニング
入力データ X, 正解データ T, ミニバッチサイズは1としデータ1個毎に結合の重みを変更します。 データ4個では学習しきれませんので同じデータで 30 回くり返し学習させます。 学習はモデルの fit メソッドで行います。
model.fit(X, T, epochs=30, batch_size=1)
Epoch 1/30 4/4 [==============================] - 0s - loss: 0.4352 Epoch 2/30 4/4 [==============================] - 0s - loss: 0.4204 Epoch 3/30 4/4 [==============================] - 0s - loss: 0.4079 :::
学習したモデルのテスト
ニューラルネットは入力の値に応じて何かを出力する機械とみなせますが、これは入力のデータから何かを予測 (predict) しているとも考えられます。
そして今回のように事前に決めた形式内のあらゆるデータに対して 0 または 1 で表明していますので、2値への分類を行っているともみなせます。
このように学習済みのモデルを使って分類を行わせる処理を Keras では predict_classes にて行います。
実際にトレーニングの入力データ X を再度流用して入力データとし、ミニバッチは 1 で分類させてみましょう。
Y = model.predict_classes(X, batch_size=1)
1/4 [======>.......................] - ETA: 0s
分類したデータ Y とトレーニングの正解データ T を numpy の配列比較で各要素の比較をします
print(Y == T)
[[ True] [ True] [ True] [ True]]
Y が T と要素毎に一致していますので、ただしく分類されたことがわかります。最後にコードをまとめておきます。
# モジュール読み込み
import numpy as np
from keras.models import Sequential
from keras.layers import Dense, Activation
from keras.optimizers import SGD
# 乱数を固定値で初期化
np.random.seed(0)
# シグモイドの単純パーセプトロン作成
model = Sequential()
model.add(Dense(input_dim=2, units=1))
model.add(Activation('sigmoid'))
model.compile(loss='binary_crossentropy', optimizer=SGD(lr=0.1))
# トレーニング用入力 X と正解データ T
X = np.array( [[0,0],
[0,1],
[1,0],
[1,1]] )
T = np.array( [[0],
[1],
[1],
[1]] )
# トレーニング
model.fit(X, T, epochs=30, batch_size=1)
# トレーニングの入力を流用して実際に分類
Y = model.predict_classes(X, batch_size=1)
print()
print("TEST")
print(Y == T)
XOR 回路も学習してみる
OR 回路の次は XOR 回路も学習させてみましょう。
モデルの構築は全く同じで、X が 1,1 の場合の T を 0 に変更しただけです。
# トレーニング用入力 X と正解データ T
X = np.array( [[0,0],
[0,1],
[1,0],
[1,1]] )
T = np.array( [[0],
[1],
[1],
[0]] ) # ここだけ変更
# トレーニング
model.fit(X, T, epochs=30, batch_size=1) # エポックを増やして何度か試しましょう
Epoch 1/3000 4/4 [==============================] - 0s - loss: 1.1031 Epoch 2/3000 4/4 [==============================] - 0s - loss: 1.0478 Epoch 3/3000 4/4 [==============================] - 0s - loss: 0.9988 : : : : : : : : Epoch 3000/3000 4/4 [==============================] - 0s - loss: 0.7186 1/4 [======>.......................] - ETA: 0s TEST [[False] [False] [False] [ True]]
OR と同じ epochs=30 で学習できませんでしたので例えば 3000 に増やしてみますが、どこまで増やしても正しく全て True になることはありません。
これは一層だけの単純パーセプトロン(ロジスティック回帰)は 線形分離 可能な問題しか学習出来ないという特性があるためです。
次回第3回は12月26日予定で 「線形分離と多層パーセプトロン」 について解説します。少しディープラーニングっぽい話になってきますのでご期待ください!



