入門 Keras (6) 学習過程の可視化とパラメーターチューニング – MNIST データ

連載一覧

• 入門 Keras (1) Windows に Tensorflow と Keras をセットアップ
• 入門 Keras (2) パーセプトロンとロジスティック回帰
• 入門 Keras (3) 線形分離と多層パーセプトロン
• 入門 Keras (4) 多クラス分類 – Iris データを学習する
• 入門 Keras (5) 学習済みモデルと Flask で API サービスを作る
• 入門 Keras (6) 学習過程の可視化とパラメーターチューニング – MNIST データ

第6回は学習過程の可視化を通して様々なパラメーターチューニングの手法について解説していきます。テーマとする問題には機械学習のベンチマークとして定番な、手書きの数字を認識させる MNIST を用います。

MNISTデータの取得

MNIST のデータはいろんなところでホストされていますが、Keras にも用意されていますのでそちらを使います。 mnist.load_data で訓練用データと検証用データに分かれて取得することが出来ます。

from keras.datasets import mnist
# x1 : 入力データ
# t1 : 正解データ（ターゲット）
# ex1 : 評価用入力データ
# et1 : 評価用正解データ（ターゲット）
(x1, t1), (ex1, et1) = mnist.load_data()

shape を使って入力データ x1 とターゲット t1 の形を確認します。

x1.shape
(60000, 28, 28)

t1.shape
(60000,)

本連載第5回までの Keras の使い方として、入力データには入力1個を1要素としてデータ全体も配列になっている二次元配列を使っていました。一方この mnist データは (60000,28,28) の三次元の配列になっています。まずは 6万個のデータの最初の1個を表示してみます。
自動の折り返しを抑制したいので1行の要素数 28、行の幅は 200 文字まで許容するように numpy を設定し表示させます。

import numpy as np
np.set_printoptions(edgeitems=28)
np.core.arrayprint._line_width = 200
print(x1[0])

ピクセル毎に 256階調で表示された文字 S の様に見えますね！　このデータを reshape を使って 60000, 28^2 の二次元配列の入力データ x2 と評価用入力 ex2 に変換します。

x2 = x1.reshape(len(x1), x1[0].size)  # 60000, 28x28 に
ex2 = ex1.reshape(len(ex1), ex1[0].size)

x2.shape, ex2.shape
((60000, 784), (10000, 784))

訓練用ターゲット t1 も確認してみましょう。

t1[0]
5

S ではなく数字の 5 でした！ 入門 Keras (4) 多クラス分類 – Iris データ でやったように訓練用ターゲット t1 と評価用ターゲット et1 の両方をスカラー値からベクトル t2, et2 に to_categorical で変換します。

from keras.utils import np_utils
t2 = np_utils.to_categorical(t1)
et2 = np_utils.to_categorical(et1)
# 訓練用と評価用から1個づつ表示
print(t2[0])
print(et2[0])

[ 0.  0.  0.  0.  0.  1.  0.  0.  0.  0.]
[ 0.  0.  0.  0.  0.  0.  0.  1.  0.  0.]

モデルの作成と学習

データが整いましたので、モデルを作成していきます。入力数と出力数は x2[0].size, t2[0].size で決まります。
中間層（隠し層）はとりあえず 2層として、そのユニット数も 30 で始めてみます。活性化関数も第5回まで使っている sigmoid を入力層と隠し層で使い、出力層は多クラス分類なので softmax を使います。
また学習率 lr は 0.1 としました。

from keras.layers import Dense, Activation
from keras.models import Sequential
from keras.optimizers import SGD
n_in = x2[0].size
n_out = t2[0].size
hidden_layers = 2
hidden_units = 30
activation_function='sigmoid'
learning_rate = 0.1
# モデル定義
np.random.seed(0) # 乱数を固定値で初期化し再現性を持たせる
model = Sequential()
# 入力層
model.add(Dense(hidden_units, input_dim=n_in)) # 入力層から出力するユニット数は隠し層のユニット数と同数に
model.add(Activation(activation_function))
# 隠し層
for _ in range(hidden_layers):
    model.add(Dense(hidden_units))
    model.add(Activation(activation_function))
# 出力層
model.add(Dense(n_out))
model.add(Activation('softmax'))
# モデル生成
model.compile(loss='categorical_crossentropy', optimizer=SGD(lr=learning_rate))

くり返し学習させる epochs は 5 で、ミニバッチサイズは 50 としました。第4回までと同じく model.fit で学習させ、model.predict_classes で分類させてみます。

epochs = 5
batch_size = 50
model.fit(x2, t2, epochs=epochs, batch_size=batch_size)
Epoch 1/5
60000/60000 [==============================] - 3s - loss: 1.5952
Epoch 2/5
60000/60000 [==============================] - 3s - loss: 1.1840
Epoch 3/5
60000/60000 [==============================] - 3s - loss: 1.0276
Epoch 4/5
60000/60000 [==============================] - 3s - loss: 0.9782
Epoch 5/5
60000/60000 [==============================] - 3s - loss: 0.9536

result = model.predict_classes(ex2, batch_size=batch_size)
print()
print("**** RESULT ****")
_, et3 = np.where(et2 > 0) # to_categorical の逆変換
print(result == et3)
10000/10000 [==============================] - 0s
**** RESULT ****
[ True  True  True  True  True  True False  True False  True  True  True False  True  True False False  True False  True  True  True False False  True  True  True  True ...,  True  True  True False
  True  True  True  True False  True False  True  True False  True  True False  True  True False False False  True False  True  True False  True]

True の数を合計して正答率を計算すると約 65% でした。

sum(result == et3) / 10000
0.65449999999999997

学習を評価する指標

ここまでは実際に分類させた結果を集計して学習の評価を行ってきました。機械学習の評価の指標には 正解率(accuracy), 適合率(precision), 再現率(recall), が代表的です。これらの指標の計算には、まず結果を4つのパターンに分類します。

• 正解が 1 のときに正しく 1 と予測 真陽性(true positive)
• 正解が 1 のときに誤って 0 と予測 偽陰性(false negative)
• 正解が 0 のときに誤って 1 と予測 偽陽性(false positive)
• 正解が 0 のときに正しく 0 と予測 真陰性(true negative)

機械学習の正しさの指標はこれらの分類を使って計上します。
例として「ある病気の場合に真になる検査」の場合の分類を表にします。

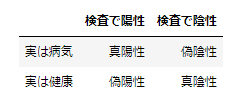
適合率(precision)

適合率は 真陽性 / (真陽性 + 偽陽性) で求められます。前述の表の例で解釈すると「検査で陽性の場合に本当に病気だった確率」と言えます。検査で陽性にもかからず病気ではないケースを最小化するのを目的とするケースで、病気であると予測した結果がいかに正確であるかに焦点をあてた指標です。

再現率(recall)

計算式は 真陽性 / (真陽性 + 偽陰性) になります。表では「実際に病気だった人が検査で正しく陽性になる確率」と言えます。病気にも関わらず検査で発見されない（陰性になる）ケースを最小化するのを目的としたケースで、実際に真となる状態（病気であること）を漏れずに網羅出来ているかどうかに焦点をあてた指標になります。

正解率 (accuracy)

(真陽性 + 真陰性) / (真陽性 + 偽陰性 + 偽陽性 + 真陰性) が計算式で、全てのパターンを考慮して「正しかった割合」を計算します。
病気と検査の関係の場合、敏感に陽性になるような検査をつくれば再現率は上がります が、適合率や正解率は下がります。 一方、群衆の中から特定の人を見つけ出すなど、 予測や分類の結果の正しさが何より重視されるケースでは、再現率や正解率より適合率が重視されます。
本記事での指標としては accuracy を使いますが、全てのパターンで正解率 (accuracy) を追求するより好ましい指標のケースもあるという点は覚えておきましょう。

Keras 内で評価を測定する

モデル作成時にどういう指標を評価するかを metrics パラメータで設定します。デフォルトで損失関数の評価値 ‘loss’ は設定されていますので今回は model.compile 文で正解率 ‘accuracy’ を追加し model.fit を実行します。

# モデル生成
model.compile(loss='categorical_crossentropy', optimizer=SGD(lr=learning_rate), metrics=['accuracy'])

Epoch 1/5
60000/60000 [==============================] - 3s - loss: 1.6042 - acc: 0.5216
Epoch 2/5
60000/60000 [==============================] - 3s - loss: 1.0757 - acc: 0.6313
Epoch 3/5
60000/60000 [==============================] - 3s - loss: 1.0780 - acc: 0.6272
Epoch 4/5
60000/60000 [==============================] - 4s - loss: 1.0071 - acc: 0.6490
Epoch 5/5
60000/60000 [==============================] - 4s - loss: 0.9256 - acc: 0.6879

model の metrics_names でどのような評価結果が入っているのかリスト出来ますので確認してみます。

model.metrics_names
['loss', 'acc']

loss と acc の2種があるのが確認出来ました。
ここまで予想や分類といった出力を得るには model.predit_classes を使いましたが、評価データ ex2 と評価ターゲット et2 を使って評価だけを実行する model.evaluate を代わりに実行します。実行すると、前述どおりloss と accuracy の結果を返してくれます。

'''
結果評価
'''
result = model.evaluate(ex2, et2)
print("**** RESULT ****")
print("Accuracy = ", result[1]) # 2つ目が acc

 9952/10000 [============================>.] - ETA: 0s**** RESULT ****
Accuracy =  0.6583

学習過程の可視化

5 回訓練を繰り返した後評価データで 65% に到達しましたが、その途中の経過を数値ではなくグラフで見てみましょう。学習させる model.fit のパラメーターに validation_data という配列で評価データとターゲットを与えておくと、model.fit の返り値の history オブジェクトに epoch 毎の訓練データでの評価と、validation_data での評価とそれぞれの結果を記録してくれます。

result = model.fit(x2, t2, epochs=epochs, batch_size=batch_size, validation_data=(ex2, et2)) # 評価用データを付けて学習

rain on 60000 samples, validate on 10000 samples
Epoch 1/5
60000/60000 [==============================] - 4s - loss: 1.5800 - acc: 0.5257 - val_loss: 1.0040 - val_acc: 0.6766
Epoch 2/5
60000/60000 [==============================] - 4s - loss: 1.0218 - acc: 0.6586 - val_loss: 0.9894 - val_acc: 0.6380
Epoch 3/5
60000/60000 [==============================] - 4s - loss: 0.9357 - acc: 0.6805 - val_loss: 0.9275 - val_acc: 0.6805
Epoch 4/5
60000/60000 [==============================] - 4s - loss: 0.9856 - acc: 0.6612 - val_loss: 1.0626 - val_acc: 0.6275
Epoch 5/5
60000/60000 [==============================] - 4s - loss: 1.0896 - acc: 0.6250 - val_loss: 1.0264 - val_acc: 0.6523

result.history.keys() # ヒストリデータのラベルを見てみる
dict_keys(['val_acc', 'acc', 'val_loss', 'loss'])

val と付いているのが validation_data に対して評価で、付いていないのは訓練データでの評価になります。データを matplotlib を使ってグラフにしてみましょう。ｘ軸は epcoch 数、y軸は正解率 (accuracy) とします。X軸の epoch 数は range() を使って 1 から epochs まで続く整数を生成します。

import matplotlib.pyplot as plt
%matplotlib inline
plt.plot(range(1, epochs+1), result.history['acc'], label="training")
plt.plot(range(1, epochs+1), result.history['val_acc'], label="validation")
plt.xlabel('Epochs')
plt.ylabel('Accuracy')
plt.legend()
plt.show()

チューニング：学習率

結果をグラフで見ると訓練データの正確性が3回目以降は低下、評価データの方も向上する傾向が見えない状況となっています。このようになるケースはいろいろありますが、まず考えられるのは訓練データに対して学習しすぎてしまうという 過学習 が考えられます。また、このケースでは1回目の epoch から評価データで 68% の正確性を出していることから 学習速度が早すぎる 可能性があります。
まずは 0.1 に設定してあった learning_rate を 0.01 に落としてみましょう。

learning_rate = 0.01 # 学習率を 0.01 に下げる

Train on 60000 samples, validate on 10000 samples
Epoch 1/5
60000/60000 [==============================] - 4s - loss: 2.2708 - acc: 0.1920 - val_loss: 2.2273 - val_acc: 0.2869
Epoch 2/5
60000/60000 [==============================] - 4s - loss: 2.1733 - acc: 0.4051 - val_loss: 2.1017 - val_acc: 0.5216
Epoch 3/5
60000/60000 [==============================] - 4s - loss: 1.9935 - acc: 0.5533 - val_loss: 1.8595 - val_acc: 0.6021
Epoch 4/5
60000/60000 [==============================] - 4s - loss: 1.6966 - acc: 0.6413 - val_loss: 1.5178 - val_acc: 0.6977
Epoch 5/5
60000/60000 [==============================] - 4s - loss: 1.3493 - acc: 0.7214 - val_loss: 1.1871 - val_acc: 0.7624

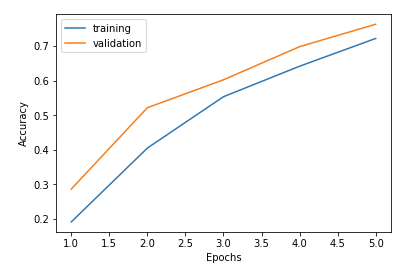
Accuracy が安定して上昇していく結果になりました。 またグラフを見ますとまだまだ向上し続ける途中の形に読み取れますので、単純に epochs=10 にしてみます。

Train on 60000 samples, validate on 10000 samples
Epoch 1/10
60000/60000 [==============================] - 5s - loss: 2.2715 - acc: 0.1900 - val_loss: 2.2284 - val_acc: 0.2835
Epoch 2/10
60000/60000 [==============================] - 5s - loss: 2.1748 - acc: 0.4076 - val_loss: 2.1031 - val_acc: 0.5161
Epoch 3/10
60000/60000 [==============================] - 4s - loss: 1.9957 - acc: 0.5497 - val_loss: 1.8628 - val_acc: 0.5973
Epoch 4/10
60000/60000 [==============================] - 4s - loss: 1.6966 - acc: 0.6432 - val_loss: 1.5153 - val_acc: 0.6969
Epoch 5/10
60000/60000 [==============================] - 4s - loss: 1.3458 - acc: 0.7229 - val_loss: 1.1804 - val_acc: 0.7573
Epoch 6/10
60000/60000 [==============================] - 5s - loss: 1.0689 - acc: 0.7741 - val_loss: 0.9601 - val_acc: 0.8008
Epoch 7/10
60000/60000 [==============================] - 4s - loss: 0.8917 - acc: 0.8078 - val_loss: 0.8263 - val_acc: 0.8235
Epoch 8/10
60000/60000 [==============================] - 4s - loss: 0.7783 - acc: 0.8260 - val_loss: 0.7451 - val_acc: 0.8325
Epoch 9/10
60000/60000 [==============================] - 5s - loss: 0.6991 - acc: 0.8389 - val_loss: 0.6528 - val_acc: 0.8501
Epoch 10/10
60000/60000 [==============================] - 5s - loss: 0.6490 - acc: 0.8468 - val_loss: 0.6215 - val_acc: 0.8597

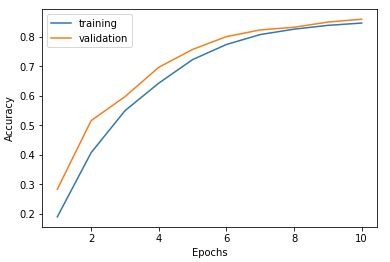
Accuracy は 85%, epoch の 10 回目でグラフも頂上に達してきたように見えます。 このまま epoch を増やしていっても向上するのは僅かですので、別のアプローチでチューニングしてみます。

チューニング：中間層追加

次に中間層を追加し 10 にしてみます。 hidden_layers=10 に設定を変更し実行します。

Train on 60000 samples, validate on 10000 samples
Epoch 1/10
60000/60000 [==============================] - 5s - loss: 2.3079 - acc: 0.1101 - val_loss: 2.3014 - val_acc: 0.1135
Epoch 2/10
60000/60000 [==============================] - 5s - loss: 2.3016 - acc: 0.1113 - val_loss: 2.3012 - val_acc: 0.1135
Epoch 3/10
60000/60000 [==============================] - 5s - loss: 2.3017 - acc: 0.1117 - val_loss: 2.3011 - val_acc: 0.1135
Epoch 4/10
60000/60000 [==============================] - 6s - loss: 2.3017 - acc: 0.1122 - val_loss: 2.3015 - val_acc: 0.1135
Epoch 5/10
60000/60000 [==============================] - 5s - loss: 2.3016 - acc: 0.1121 - val_loss: 2.3014 - val_acc: 0.1135
Epoch 6/10
60000/60000 [==============================] - 5s - loss: 2.3017 - acc: 0.1123 - val_loss: 2.3015 - val_acc: 0.1135
Epoch 7/10
60000/60000 [==============================] - 6s - loss: 2.3017 - acc: 0.1120 - val_loss: 2.3010 - val_acc: 0.1135
Epoch 8/10
60000/60000 [==============================] - 6s - loss: 2.3017 - acc: 0.1121 - val_loss: 2.3013 - val_acc: 0.1135
Epoch 9/10
60000/60000 [==============================] - 6s - loss: 2.3017 - acc: 0.1123 - val_loss: 2.3012 - val_acc: 0.1135
Epoch 10/10
60000/60000 [==============================] - 6s - loss: 2.3017 - acc: 0.1119 - val_loss: 2.3016 - val_acc: 0.1135

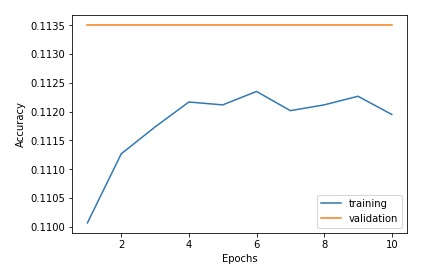
訓練、評価ともまったく学習出来なくなってしまいました。 あらゆる入力値に対して 0 ～ 1 の値を返すシグモイド関数の中間層を重ねたことで、信号の特徴自体が減ってしまう勾配消失問題が発生していた可能性が考えられます。

チューニング：活性化関数

ステップ関数のようにある閾値以上になると発火しつつ、入力値に応じた線形な値で出力する relu 関数という活性化関数があります。

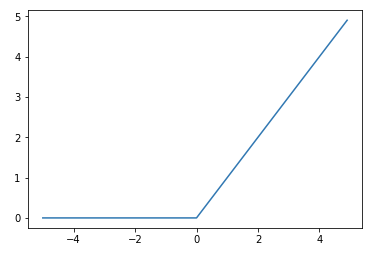
勾配消失問題には relu 関数を活性化関数に使う事で解消できる可能性がありますので使ってみます。

activation_function='relu' # 活性化関数を ReLU にする

Train on 60000 samples, validate on 10000 samples
Epoch 1/10
60000/60000 [==============================] - 7s - loss: 0.6615 - acc: 0.7911 - val_loss: 0.3966 - val_acc: 0.8831
Epoch 2/10
60000/60000 [==============================] - 6s - loss: 0.2943 - acc: 0.9175 - val_loss: 0.2739 - val_acc: 0.9187
Epoch 3/10
60000/60000 [==============================] - 6s - loss: 0.2368 - acc: 0.9333 - val_loss: 0.2453 - val_acc: 0.9311
Epoch 4/10
60000/60000 [==============================] - 6s - loss: 0.2028 - acc: 0.9426 - val_loss: 0.1969 - val_acc: 0.9413
Epoch 5/10
60000/60000 [==============================] - 8s - loss: 0.1789 - acc: 0.9500 - val_loss: 0.2424 - val_acc: 0.9312
Epoch 6/10
60000/60000 [==============================] - 9s - loss: 0.1639 - acc: 0.9534 - val_loss: 0.1869 - val_acc: 0.9469
Epoch 7/10
60000/60000 [==============================] - 8s - loss: 0.1515 - acc: 0.9561 - val_loss: 0.1781 - val_acc: 0.9496
Epoch 8/10
60000/60000 [==============================] - 8s - loss: 0.1390 - acc: 0.9597 - val_loss: 0.1615 - val_acc: 0.9532
Epoch 9/10
60000/60000 [==============================] - 8s - loss: 0.1329 - acc: 0.9621 - val_loss: 0.1637 - val_acc: 0.9535
Epoch 10/10
60000/60000 [==============================] - 7s - loss: 0.1232 - acc: 0.9638 - val_loss: 0.1848 - val_acc: 0.9455

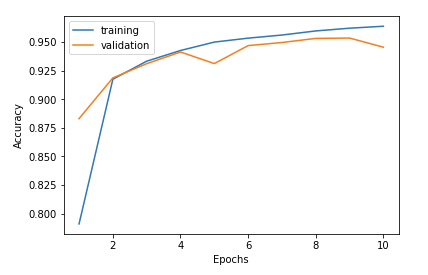
最初は約 85% で頭打ちになっていた学習率をチューニングしたことで約 95% に上げることが出来ました！
最後に今回のコードをまとめておきます。

from keras.datasets import mnist
from keras.utils import np_utils
from keras.layers import Dense, Activation
from keras.models import Sequential
from keras.optimizers import SGD
import matplotlib.pyplot as plt
%matplotlib inline
# x1 : 入力データ
# t1 : 正解データ（ターゲット）
# ex1 : 評価用入力データ
# et1 : 評価用正解データ（ターゲット）
(x1, t1), (ex1, et1) = mnist.load_data()
t2 = np_utils.to_categorical(t1)
et2 = np_utils.to_categorical(et1)
n_in = x2[0].size
n_out = t2[0].size
hidden_layers = 10
hidden_units = 30
activation_function='relu'
learning_rate = 0.01
epochs = 10
batch_size = 50
# モデル定義
np.random.seed(0) # 乱数を固定値で初期化し再現性を持たせる
model = Sequential()
# 入力層
model.add(Dense(hidden_units, input_dim=n_in)) # 入力層から出力するユニット数は隠し層のユニット数と同数に
model.add(Activation(activation_function))
# 隠し層
for _ in range(hidden_layers):
    model.add(Dense(hidden_units))
    model.add(Activation(activation_function))
# 出力層
model.add(Dense(n_out))
model.add(Activation('softmax'))
# モデル生成
model.compile(loss='categorical_crossentropy', optimizer=SGD(lr=learning_rate), metrics=['accuracy'])
# 学習
result = model.fit(x2, t2, epochs=epochs, batch_size=batch_size, validation_data=(ex2, et2))
# グラフ化
plt.plot(range(1, epochs+1), result.history['acc'], label="training")
plt.plot(range(1, epochs+1), result.history['val_acc'], label="validation")
plt.xlabel('Epochs')
plt.ylabel('Accuracy')
plt.legend()
plt.show()

終わりなきパラメーターチューニング

今回紹介したチューニングは入口部分をほんの少し覗いただけのもので、実際には ニューラルネットの最初の状態をあらかじめ 0 ではなく適したものに初期化しておくことで性能を高める 初期化方法のチューニング、入力データの絶対値的な大きさが学習に影響しないようにする データの正規化、局所最適化に陥ることを防止するための ニューロンのドロップアウト など、 様々なチューニングが必要になります。

まとめ

第1回からここまでは全結合で層状になっている多層パーセプトロンを中心に紹介してきました。画像などある一つの入力に対しての学習で効果を発揮するものでした。 次回 2月20日(火) 予定の第7回は連載の最終回として、時系列データや言語など、連続した値に関しての予測を可能にするリカレントニューラルネットワークについて解説させて頂く予定です。ご期待ください。