入門 Keras (7) 最終回：リカレントニューラルネットワークを体験する

連載一覧

連載最終回となる第7回は、時系列データの予測や音声認識、言語の翻訳などディープラーニングの様々なシーンで活躍しているリカレントニューラルネットワーク(RNN) について Keras の SimpleRNN を用いて体験します。

リカレントニューラルネットワーク (RNN)

時系列、つまり順序に意味のあるデータを学習させるのに適したニューラルネットワークがリカレントニューラルネットワーク (Recurrent Neural Network) です。繰り返しを意味する Recurrent という名前にあるように、順序データの学習を行うためにニューロンの出力を自分の次の入力に足して処理していくのが特徴です。

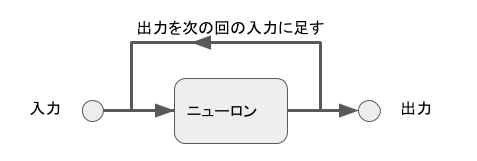
例えば 100 個の順序データがあったとして、それを1回あたり10個のデータを1回の入力として

1から10までのデータ
2から11までのデータ
* * *
91 から 100 までのデータ

のように1個づつずらしたデータ群を1個の入力として学習させていきます。

ノイズ入り sin 波

時系列データ予測の入門として定番ともいえる「ノイズ入り sin 波の予測」を Keras の SimpleRNN で行ってみましょう。まずは sin 波のデータ生成します。1周期は 100 個のデータで構成されているとして、2周期分生成してみます。

import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline
def sin2p(x, t=100):
    return np.sin(2.0 * np.pi * x / t) # sin(2πx/t) t = 周期
def sindata(t=100, cycle=2):
    x = np.arange(0, cycle*t) # 0 から cycle * t 未満の数
    return sin2p(x)
plt.plot(sindata(100, 2)) # 1周期100個データ、2周期分
plt.show()

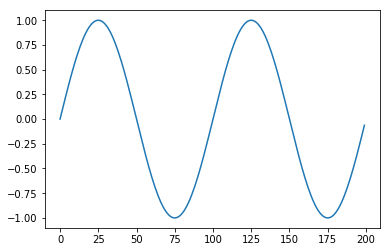
あまりにも規則正しいと簡単すぎますのでこのデータにノイズを加える noisy 関数を作ります。元のデータに対して、最小値と最大値 (min, max) の幅でランダムな数字を加えます。

def noisy(Y, noise_range=(-0.05, 0.05)):
    noise = np.random.uniform(noise_range[0], noise_range[1], size=Y.shape)
    return Y + noise
plt.plot(noisy(sindata(100, 2), (-0.05, 0.05) ))
plt.show()

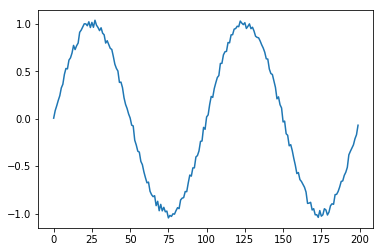
訓練と評価用にデータを加工

リスト状、つまり1次元配列のデータを用意することはできましたが、これを1個の入力が一定の長さの逐次データ群となるよう、データをインデックスの 0 から 10個、1から10個、2から10個、というようにずらしたデータ群となるように成形していきます。
また SimpleRNN は入力データとして (データ全体の数、入力1個のデータの数、入力1個のデータの次元数）で構成された numpy の3次元配列として与える必要がありますので合うように加工します。
データは scikit-learn のシャッフルしない設定にした train_test_split で先頭8割を訓練に、残り2割を評価用に分割します。

from sklearn.model_selection import train_test_split
np.random.seed(0)
rawdata = noisy(sindata(100,2), (-0.05, 0.05)) # 2周期分のノイズあり sin 波データを生成
inputlen = 20 # 1入力データはデータ 20 個としました
input=[]
target=[]
for i in range(0, len(rawdata) - inputlen):  # range(0, 180)   0 .. 179 の 180回実行
    input.append( rawdata[i:i+inputlen] )  # [i:i+20] のスライスで i から i+19 の20個を入力データに追加
    target.append( rawdata[i+inputlen] )  # [i+20] がその直前までのデータ群 [i:i+20] の正解値となるのでターゲットに追加
# numpy の3次元配列に変換
X = np.array(input).reshape(len(input), inputlen, 1) # 入力データ (180, 20, 1)
Y = np.array(target).reshape(len(input), 1) # ターゲット (180, 1)
# トレーニングと評価用にデータを 8:2 に分割します。デフォルトがシャッフルなのでしないように
x, val_x, y, val_y = train_test_split(X, Y, test_size=int(len(X) * 0.2), shuffle=False)
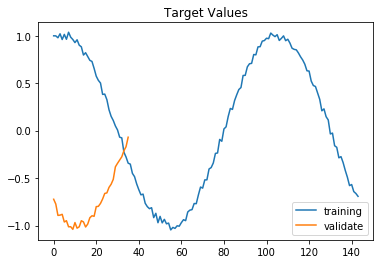
# 訓練データの正解値 y と評価用データの正解値 val_y のグラフ
plt.plot(y, label="training")
plt.plot(val_y, label="validate")
plt.title('Target Values')
plt.legend()
plt.show()

SimpleRNN で学習させる

入力の数と出力の数（今回のケースではそれぞれ１）、隠し層の数、epochs 数、batch_size などは前回までの多層パーセプトロンと同様の考え方になります。
誤差関数には平均二乗誤差の mean_squard_error を使い、最適化関数には学習率 0.01 の Adaptive Moment Estimation (Adam) を用いています。初期パラメータ beta_1 と beta_2 は Adam ではよく使われている 0.9, 0.999 で開始しています。
活性化関数には線形の linear を用いて、結合の重みの初期値は一様に 0 ではなくランダムな値 random_normal で初期化しています。
今回は体験が目的ということで割愛しましたが、これら最適化アルゴリズムやパラメータに関しての詳しい解説は勾配効果法の最適化アルゴリズムを概観するなどの記事をご参考にしてください。

from keras.layers.recurrent import SimpleRNN
from keras.models import Sequential
from keras.optimizers import Adam
from keras.layers import Dense, Activation
n_in = 1
n_hidden = 20
n_out = 1
epochs = 10
batch_size = 10
model=Sequential()
model.add(SimpleRNN(n_hidden, input_shape=(inputlen, n_in), kernel_initializer='random_normal'))
model.add(Dense(n_out, kernel_initializer='random_normal'))
model.add(Activation('linear'))
model.compile(loss='mean_squared_error', optimizer=Adam(lr=0.01, beta_1=0.9, beta_2=0.999))
model.fit(x, y, batch_size=batch_size, epochs=epochs, validation_data=(val_x, val_y))

Train on 144 samples, validate on 36 samples
Epoch 1/10
144/144 [==============================] - 1s - loss: 0.3583 - val_loss: 0.0560
Epoch 2/10
144/144 [==============================] - 0s - loss: 0.0451 - val_loss: 0.0055
Epoch 3/10
144/144 [==============================] - 0s - loss: 0.0082 - val_loss: 0.0040
Epoch 4/10
144/144 [==============================] - 0s - loss: 0.0037 - val_loss: 0.0030
Epoch 5/10
144/144 [==============================] - 0s - loss: 0.0022 - val_loss: 0.0021
Epoch 6/10
144/144 [==============================] - 0s - loss: 0.0019 - val_loss: 0.0018
Epoch 7/10
144/144 [==============================] - 0s - loss: 0.0017 - val_loss: 0.0016
Epoch 8/10
144/144 [==============================] - 0s - loss: 0.0018 - val_loss: 0.0016
Epoch 9/10
144/144 [==============================] - 0s - loss: 0.0018 - val_loss: 0.0015
Epoch 10/10
144/144 [==============================] - ETA: 0s - loss: 0.001 - 0s - loss: 0.0017 - val_loss: 0.0015

学習済みモデルを使って予測する

sin 波の断片部分（１入力データ群と同じ 20 個の逐次データ）を元に、残りの部分を予測してみます。
トレーニングの時と同様、20個データを一つの塊として、データ一つ分ずらしながら予測していきますので、 20回めの予測以後の先は元の入力データは一つも使わずに、自分が予測したデータを使ってまたその先を予測する、という状態になります。

# 本来は評価データを使うべきですが、グラフの見栄え的に元データの左端を与えて
# 右側を予測させたかったので訓練データ x の先頭を与えました
in_ = x[:1] # x の先頭 (1,20,1) 配列
# グラフで予測データ（オレンジ）が入力データ（緑）の後に来るように
# 予測データの先頭に None を20個入れてあります
predicted = [None for _ in range(inputlen)]
for _ in range(len(rawdata) - inputlen):
    out_ = model.predict(in_) # 予測した値 out_ は (1,1) 配列
    # in_ を (20,1) 配列に変換し、先頭1個をスライスして削り、末尾に out_ を足す。
    # 最後に再度 (1,20,1) 配列に変換して、全体を次の in_ にする
    in_ = np.concatenate( (in_.reshape(inputlen, n_in)[1:], out_), axis=0 ).reshape(1, inputlen, n_in)
    # out_ は (1,1) 配列なので任意の長さの一次元配列に変換する reshape(-1) をかけてから予測データに追加
    predicted.append(out_.reshape(-1))
plt.title('Predict sin wave')
plt.plot(rawdata, label="original")
plt.plot(predicted, label="predicted")
plt.plot(x[0], label="input")
plt.legend()
plt.show()

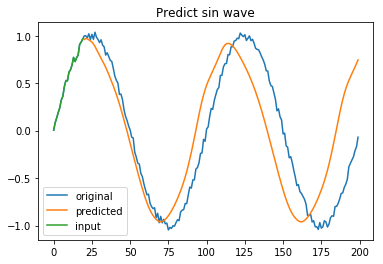
緑が入力データで、オレンジの線が自分で予測したデータになります。
予測した値を使ってまた次の予測を行っていますので、次第に誤差が大きくなっていく現象をよく観察することができました！

まとめ

このように時系列データなど逐次データに対しての学習を可能にするリカレントニューラルネットワークですが、1個の入力データ群とすることのできる1回のデータ量を多くすることが難しいという欠点があります。この欠点を解消するために考えられたのが Long Short-Term Memory (LSTM) で、LSTM の構造が複雑だったのでその改良として提案されているのが ~~Generative Adversarial Network (GAN)~~ Gated Recurrent Unit (GRU) になります。リカレントニューラルネットワークの本格的な応用の場面では LSTM, ~~GAN~~ GRU などが使われるているようです。(2018/2/23: GAN を GRU に訂正）
本連載は以上で最後となります。ここまで紹介してきましたように Keras を使うと複雑な理論や計算に裏付けられたニューラルネットを簡単に記述し使うことが出来ます。みなさんも是非ご活用ください！
（末尾に今回のコードを再度まとめておきます）

import numpy as np
import matplotlib.pyplot as plt
from sklearn.model_selection import train_test_split
from keras.layers.recurrent import SimpleRNN
from keras.models import Sequential
from keras.optimizers import Adam
from keras.layers import Dense, Activation
%matplotlib inline
def sin2p(x, t=100):
    return np.sin(2.0 * np.pi * x / t) # sin(2πx/t) t = 周期
def sindata(t=100, cycle=2):
    x = np.arange(0, cycle*t) # 0 から cycle * t 未満の数
    return sin2p(x)
# データ準備
np.random.seed(0)
rawdata = noisy(sindata(100,2), (-0.05, 0.05))
inputlen = 20
input=[]
target=[]
for i in range(0, len(rawdata) - inputlen):
    input.append( rawdata[i:i+inputlen] )
    target.append( rawdata[i+inputlen] )
X = np.array(input).reshape(len(input), inputlen, 1)
Y = np.array(target).reshape(len(input), 1)
x, val_x, y, val_y = train_test_split(X, Y, test_size=int(len(X) * 0.2), shuffle=False)
# トレーニング
n_in = 1
n_hidden = 20
n_out = 1
epochs = 10
batch_size = 10
model=Sequential()
model.add(SimpleRNN(n_hidden, input_shape=(inputlen, n_in), kernel_initializer='random_normal'))
model.add(Dense(n_out, kernel_initializer='random_normal'))
model.add(Activation('linear'))
model.compile(loss='mean_squared_error', optimizer=Adam(lr=0.01, beta_1=0.9, beta_2=0.999))
model.fit(x, y, batch_size=batch_size, epochs=epochs, validation_data=(val_x, val_y))
# 予測
in_ = x[:1] # x の先頭 (1,20,1) 配列
predicted = [None for _ in range(inputlen)]
for _ in range(len(rawdata) - inputlen):
    out_ = model.predict(in_) # 予測した値 out_ は (1,1) 配列
    in_ = np.concatenate( (in_.reshape(inputlen, n_in)[1:], out_), axis=0 ).reshape(1, inputlen, n_in)
    predicted.append(out_.reshape(-1))
plt.title('Predict sin wave')
plt.plot(rawdata, label="original")
plt.plot(predicted, label="predicted")
plt.plot(x[0], label="input")
plt.legend()
plt.show()