インフィニットループ 技術ブログ

2023年01月23日 (月)

著者 ： nob

Linux PHP #3Dモデル #Linux #PHP #アート #技術記事

PHPとSDLで始めるコンピューターグラフィックス – 回転と極座標

こんにちは nobuh です。前々回と前回の２回にわたり PHP と SDL でのプリミティブな操作を使ってコンピューターグラフィックスを楽しんでいるこのシリーズ。３回目は移動や視点の操作で必須となる座標の回転と極座標表示について取り組みます！

ここまでの振り返り

少し改良

第 2 回までの 3D 表示の機能のまま、プログラムを少し改良してみました。

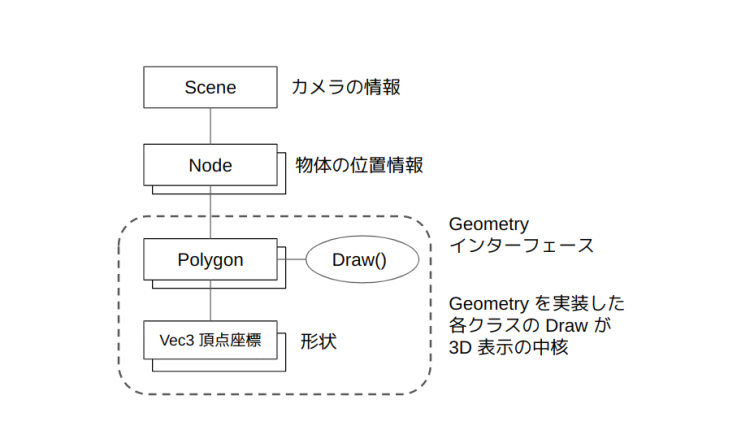
まずは 3D データを準備するときに形状と位置がごちゃまぜになっていたのを形状の情報と位置の情報に分離しました。加えてオブジェクト指向っぽく構造を整理しました。具体的には

  • Draw() メソッドを持つ描画の単位を Geometry インタフェースとします
  • 第 2 回で実装した Polygon も Geometry を実装した形にします
  • Geometry の集合体を Node とします
  • Node は物体の位置の座標を持ち、Geometry は Node の位置からの３次元座標で形状のみを表すことにしました
  • プログラム全体での Node の集合を持つものを Scene とし、視点移動のためのオフセットであるカメラの位置やイベントなど Scene で保持します

その他の変更点

  • 物体が背面にまわっても大丈夫
    • 視点が物体と通り越すとエラーになっていたのを z 軸での位置が背面にまわったジオメトリは表示しないように修正
  • Engine クラス
    • 全体は Engine クラスの Start() メソッドで実行し、Buildup() と Update() の２つの関数を実装することでデモを作れるように
  • FPS カウンター
    • 1000/60 ms 均一でディレイを入れていましたが、Update にかかった時間を計測し 60 FPS を超えそうな時に必要な Delay を入れるように
  • WASD で移動
    • 移動は矢印キーからゲームでよく使われている WASD キーに変更
<?php declare(strict_types=1);
error_reporting(E_ALL);

const SCREEN_WIDTH = 640;
const SCREEN_HEIGHT = 480;
const SCREEN_DISTANCE = SCREEN_WIDTH;

class Vec2
{
    public float $x;
    public float $y;

    public function __construct($x, $y)
    {
        $this->x = $x;
        $this->y = $y;
    }
}

class Vec3
{
    public float $x;
    public float $y;
    public float $z;

    public function __construct($x, $y, $z)
    {
        $this->x = $x;
        $this->y = $y;
        $this->z = $z;
    }
}

interface Geometry
{
    public function Draw(Scene $scene, Node $node);
}

// ジオメトリの一つとして Polygon を実装
// 生成時には Vec3 の配列を指定して使う
class Polygon implements Geometry
{
    public array $vertices;
    public Vec3 $position;

    public function __construct(array $points)
    {
        $this->vertices = $points;
    }

    // 射影投影
    public function Projection(Scene $scene, Node $node): mixed
    {
        $sp = [];  // スクリーン上の座標

        for ($i = 0; $i < count($this->vertices); $i++) {
            // 位置指定の position とカメラの offset 分を合算して
            // position を中心とした vertices の座標を生成
            $x = $this->vertices[$i]->x + $node->position->x - $scene->camera->offset->x;
            $y = $this->vertices[$i]->y + $node->position->y - $scene->camera->offset->y;
            $z = $this->vertices[$i]->z + $node->position->z - $scene->camera->offset->z;

            // $z が 0 より小さいと視点の背面なので投影しない
            if ($z > 0) {
                // 透視投影
                $xp = SCREEN_DISTANCE / $z * $x;
                $yp = SCREEN_DISTANCE / $z * $y;

                // 原点 (0,0) を画面の中心から左上に変換
                $xp = SCREEN_WIDTH / 2 + $xp;
                $yp = SCREEN_HEIGHT / 2 - $yp;

                $sp[$i] = new Vec2($xp, $yp);
            } else {
                return null;
            }
        }

        return $sp;
    }

    public function Draw(Scene $scene, Node $node): void
    {
        $sp = $this->Projection($scene, $node);

        if (is_null($sp)) {
            // 背面なので何もしない
        } else {
            // 末端の点として最初の点を再追加
            // 例：三角形の辺 p0 => p1 => p2 => p0 
            $sp[] = $sp[0];

            for ($i = 0; $i < count($sp) - 1; $i++) {
                SDL_RenderDrawLine($scene->renderer, (int)$sp[$i]->x, (int)$sp[$i]->y,
                    (int)$sp[$i+1]->x, (int)$sp[$i+1]->y);
            }
        }
    }
}

// Node は物体の位置とジオメトリを保持する
class Node
{
    public array $geometries;
    public Vec3 $position;

    public function __construct(array $geos, Vec3 $position)
    {
        $this->geometries = $geos;
        $this->position = $position;
    }
}

class Camera
{
    public Vec3 $offset;

    public function __construct()
    {
        $this->offset = new Vec3(0,0,0);
    }
}

class Scene
{
    public Camera $camera;
    public array $nodes;
    public $renderer;
    public $event;
}

class Engine
{
    public function Start()
    {
        $scene = new Scene();
        $scene->camera = new Camera();
        Buildup($scene);

        SDL_Init(SDL_INIT_VIDEO);
        $window = SDL_CreateWindow("PHP SDL 3D", SDL_WINDOWPOS_UNDEFINED,
            SDL_WINDOWPOS_UNDEFINED, SCREEN_WIDTH, SCREEN_HEIGHT, SDL_WINDOW_SHOWN);
        $scene->renderer = SDL_CreateRenderer($window, 0, SDL_RENDERER_ACCELERATED);

        $scene->event = new SDL_Event;
        $quit = false;
        while (!$quit) {
            $start = microtime(true);

            // 更新と描画の処理本体
            Update($quit, $scene);

            SDL_RenderPresent($scene->renderer);

            // 処理時間を計算して FPS 60 以上になりそうなら Delay を入れる
            $processed = (microtime(true) - $start) * 1000;
            if ($processed < 1000/60) {
                SDL_Delay(intval(1000/60 - $processed));
                $processed = (microtime(true) - $start) * 1000;
            }
            $fps = intval(1000/$processed);

            // ステータス表示
            $title = "FPS ".$fps." Camera (".$scene->camera->offset->x.","
                .$scene->camera->offset->y.",".$scene->camera->offset->z.")";
            SDL_SetWindowTitle($window, $title);
        }

        SDL_DestroyRenderer($scene->renderer);
        SDL_DestroyWindow($window);
        SDL_Quit();
    }
}
$engine = new Engine();
$engine->Start();

// シーン上のデータを作成する
function Buildup(Scene $scene)
{
    // 立方体データ
    //    2   4
    //   1   3
    //    6   8
    //   5   7
    $p1 = new Vec3(-100,100,-100);
    $p2 = new Vec3(-100,100,100);
    $p3 = new Vec3(100,100,-100);
    $p4 = new Vec3(100,100,100);
    $p5 = new Vec3(-100,-100,-100);
    $p6 = new Vec3(-100,-100,100);
    $p7 = new Vec3(100,-100,-100);
    $p8 = new Vec3(100,-100,100);
    $cube[] = new Polygon([$p1, $p2, $p4, $p3]);  
    $cube[] = new Polygon([$p1, $p2, $p6, $p5]);  
    $cube[] = new Polygon([$p2, $p4, $p8, $p6]);  
    $cube[] = new Polygon([$p3, $p4, $p8, $p7]);  
    $cube[] = new Polygon([$p1, $p3, $p7, $p5]);  
    $cube[] = new Polygon([$p5, $p6, $p8, $p7]);
    $scene->nodes[] = new Node($cube, new Vec3(0,0,1000));
    $scene->nodes[] = new Node($cube, new Vec3(300,0,2000));
    $scene->nodes[] = new Node($cube, new Vec3(-100,0,1500));
    $scene->nodes[] = new Node($cube, new Vec3(-200,0,3000));
}

// 描画処理本体
function Update(&$quit, Scene $scene)
{
    while (SDL_PollEvent($scene->event)) {
        if ($scene->event->type == SDL_MOUSEBUTTONDOWN || $scene->event->type == SDL_QUIT){
            $quit = true;
        }
        if ($scene->event->type == SDL_KEYDOWN){
            $keyboardState = SDL_GetKeyboardState($num);
            if($keyboardState[SDL_SCANCODE_W]) {
                $scene->camera->offset->z += 20.0;
            }
            if($keyboardState[SDL_SCANCODE_A]) {
                $scene->camera->offset->x -= 20.0;
            }
            if($keyboardState[SDL_SCANCODE_S]) {
                $scene->camera->offset->z -= 20.0;
            }
            if($keyboardState[SDL_SCANCODE_D]) {
                $scene->camera->offset->x += 20.0;
            }
        }
    }

    SDL_SetRenderDrawColor($scene->renderer, 0xE0, 0xF8, 0xD0, 0xFF);
    SDL_RenderClear($scene->renderer);
    SDL_SetRenderDrawColor($scene->renderer, 0x08, 0x18, 0x20, 0xFF);

    foreach ($scene->nodes as $node) {
        foreach($node->geometries as $geometry) {
            $geometry->Draw($scene, $node);
        }
    }
}

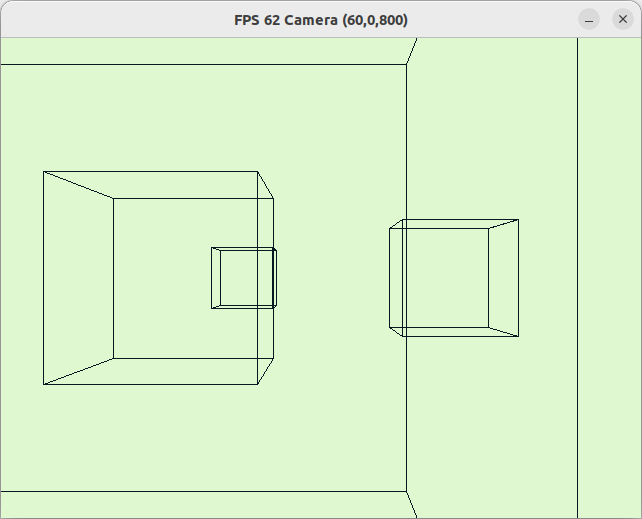
立方体を４個配置したシーンを実行してみました。FPS 表示が追加された以外は第 2 回と見た目は同じです。

視点の回転と極座標表示

ここまでの左右の移動は全て左右にスライドするような動きでした。次に左右に視点が回転するように実装します。

今やりたいのは水平面上での回転だけになりますので高さ y は無視してよく、水平面の xz 平面上での 2D の座標の回転になります。

いままで使った x,y,z による座標表示は縦横に直交した座標軸を使って表現しているため 直交座標系、直交座標表示 と言われます。それに対し原点からの距離と角度で表現したのが 極座標系、極座標表示 です。

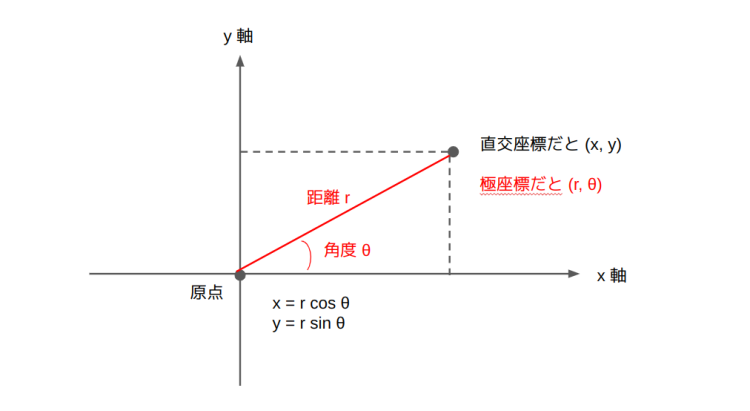
縦横の大きさは、原点からの距離を斜辺とした三角関数で求められる関係になっています。さらに上の図の x,y 座標の点を角度 +φ 回転させた場合の計算式は三角関数の加法定例を使って

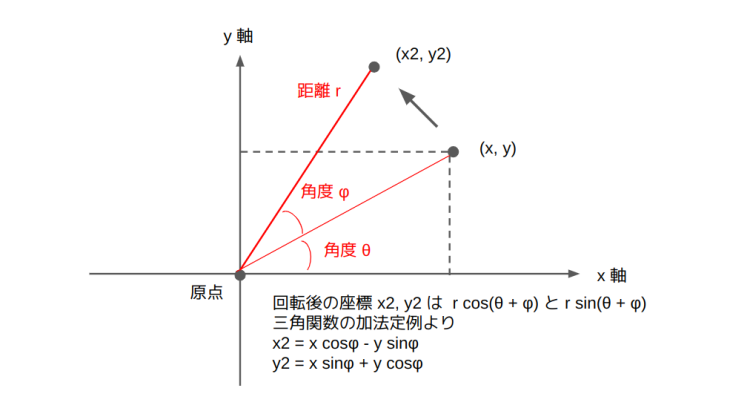
  • x2 = x cosφ – y sinφ
  • y2 = x sinφ + y cosφ

のように求められます。この極座標表示をカメラの向きや回転に応用します。 Scene でカメラの位置の他に、向きの状態を持ちます。飛行機などで使う用語ですが、回転角度は

  • 左右の傾き ロー：左手座標系の場合は前後にはしる z 軸を軸にした回転
  • 前後の傾き ピッチ：左手座標系では水平で左右にはしる x 軸を軸にした回転
  • 駒のような回転 ヨー：左手座標系の垂直 y 軸を軸にした回転
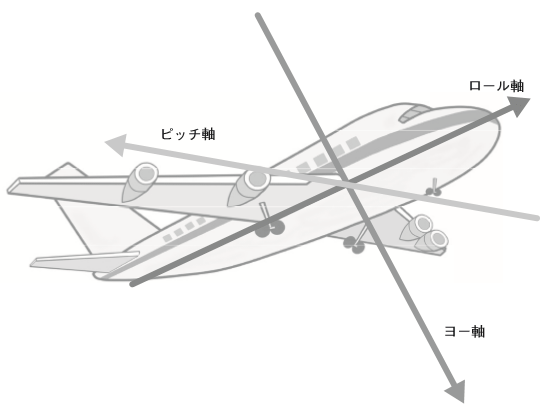
引用：https://www.buildinsider.net/small/bookkinectv2/0804

にて表現されます。カメラの角度として今回は水平面上での回転だけを実装しますので、回転角はヨーの変化のみとなりますが、y 軸での回転ということで Camera オブジェクトの Vec3 の y で保持します。

class Camera
{
    public Vec3 $offset;
    public Vec3 $rolling;

    public function __construct()
    {
        $this->offset = new Vec3(0,0,0);
        $this->rolling = new Vec3(0,0,0);
    }
}

キー入力に応じたカメラの移動ですが、まっすぐ前を向いている今まで違い角度に応じて進む x と y の変化量も三角関数で分配する必要があるのと、左右の場合はオフセット位置ではなく角度の +/- を行うよう実装します。

（移動距離の 20.0 や角度の 0.02 （ラジアン）は実機で調整した値で理論的な由来は特にありません）

        if ($scene->event->type == SDL_KEYDOWN){
            $keyboardState = SDL_GetKeyboardState($num);
            // WASD キーでカメラのオフセット前進後進と回転
            if($keyboardState[SDL_SCANCODE_W]) {
                $scene->camera->offset->z += 20.0 * cos($scene->camera->rolling->y);
                $scene->camera->offset->x -= 20.0 * sin($scene->camera->rolling->y);
            }
            if($keyboardState[SDL_SCANCODE_A]) {
                $scene->camera->rolling->y += 0.02;
            }
            if($keyboardState[SDL_SCANCODE_S]) {
                $scene->camera->offset->z -= 20.0 * cos($scene->camera->rolling->y);
                $scene->camera->offset->x += 20.0 * sin($scene->camera->rolling->y);
            }
            if($keyboardState[SDL_SCANCODE_D]) {
                $scene->camera->rolling->y -= 0.02;
            }
            // ヨーが ±180 (pi) を超えたらラップさせる
            if ($scene->camera->rolling->y < - pi()) {
                $scene->camera->rolling->y = 2.0 * pi() - $scene->camera->rolling->y;
            }
            if ($scene->camera->rolling->y > pi()) {
                $scene->camera->rolling->y = $scene->camera->rolling->y - 2.0 * pi();
            }
        }

Polygon での透視変換と描画の部分は以下のように、カメラ座標のオフセット分を引いたあとに、カメラの角度 $rolling->y 分逆方向に回転させました

            // 位置指定の position とカメラの offset 分を合算して
            // position を中心とした vertices の座標 xv,yv,zv を生成
            $xv = $this->vertices[$i]->x + $node->position->x - $scene->camera->offset->x;
            $yv = $this->vertices[$i]->y + $node->position->y - $scene->camera->offset->y;
            $zv = $this->vertices[$i]->z + $node->position->z - $scene->camera->offset->z;

            // カメラの向きの分 y 軸 (xz 平面）で逆に回転し x,z を生成
            //   x / z  = | cosθ    -sinθ | xv
            //            | sinθ    cosθ  | zv
            $x = cos(- $scene->camera->rolling->y) * $xv - sin(- $scene->camera->rolling->y) * $zv;
            $y = $yv;
            $z = sin(- $scene->camera->rolling->y) * $xv + cos(- $scene->camera->rolling->y) * $zv;

おまけでステータス表示でヨーの角度を表示するようにもしています

            // タイトルバー使ったステータス表示
            $title = "FPS ".$fps." Position (".(int)$scene->camera->offset->x.","
            .(int)$scene->camera->offset->y.","
            .(int)$scene->camera->offset->z.") Yaw ("
            .intval($scene->camera->rolling->y * 360.0 / 2.0 / pi()). "°)";
            SDL_SetWindowTitle($window, $title);

以上を実装してうごかしたみたのがこちらです！

極座標で球体を描こう

ずっと立方体を扱ってきましたが極座標をマスターしましたので、地球のような球体表示に挑戦してみます。

Polygon ジオメトリは一つの自由な多角形で、Node は Polygon を集めて一つの立体としていました。球体を描くために球体１個を Node とし、3次元上の１点を PolarDot ジオメトリとし、Node は PolarDot を多数含むという構成にしました。

尚、SDL の Acceratred Renderer の API に円を描く API がなく、代わりに四角を点に使います。

Polygon は x,y,z の座標の複数の点で表現されていましたが PolarDot は極座標を採用します。極座標は

  • r : 中心からの距離
  • θ : y軸の先からの角。天頂角と言います。
    • 緯度は赤道からの角度ですがその逆で北極からの角度と考えるとイメージしやすいです
  • φ : xz の水平面上で x 軸の先からの角。偏角と言います。
    • x 軸の先をグリニッジと見たてたときの経度と似ています。

この3つを変数に、点のサイズを加えた4変数を与えて PolarDot ジオメトリを実装します。

// 極座標表示の点のジオメトリ
class PolarDot implements Geometry
{
    // 左手系なので yの正の先を天頂（北極）方向と考える
    public float $radius; // 中心からの距離。動径。
    public float $theta;  // y軸の先からの角θ。天頂角。
    public float $phi;    // xz 平面上 x 軸の先からの角φ。偏角。
    public float $size;   // 遠近適用前の元となる点のサイズ

    public function __construct(float $radius, float $theta, float $phi, float $size)
    {
        $this->radius = $radius;
        $this->theta = $theta;
        $this->phi = $phi;
        $this->size = $size;
    }

カメラの位置と向きを相殺しての射影投影の Projection は以下になります。極座標から直交座標に変換しカメラの位置をオフセットしています。

    // 単点で構成された PolarDot を2D位置とサイズに変換して返す    
    public function Projection(Scene $scene, Node $node): mixed
    {
        // 極座標 r,θ,φ を直交座標 x,y,z に変換する
        // y = r cosθ で r sinθ が xz 平面への射影になるので
        // z = r sinθsinφ
        // x = r sinθcosφ
        // カメラ位置 $position も引いて合算する
        $y = $this->radius * cos($this->theta) + $node->position->y - $scene->camera->offset->y;
        $z = $this->radius * sin($this->theta) * sin($this->phi) + $node->position->z - $scene->camera->offset->z;
        $x = $this->radius * sin($this->theta) * cos($this->phi) + $node->position->x - $scene->camera->offset->x;

その後カメラの向きの分回転逆方向に回転しておくのは Polygon ジオメトリと同様です

        // カメラのヨー分 y 軸 (xz 平面）で逆に回転
        //   x' / z'     cosθ    -sinθ | x
        //            =  sinθ    cosθ  | z
        $rx = cos(- $scene->camera->rolling->y) * $x - sin(- $scene->camera->rolling->y) * $z;
        $rz = sin(- $scene->camera->rolling->y) * $x + cos(- $scene->camera->rolling->y) * $z;

x と z が回転したら、次に投影します。投影の際には点（四角）のサイズも合わせて縮小し、スクリーン上の x,y と点のサイズを z に入れて Vec3 で返します。

        if ($z > 0) {
            $xp = SCREEN_DISTANCE / $rz * $rx;
            $yp = SCREEN_DISTANCE / $rz * $y;
    
            // 点のサイズも同率で縮小
            $sizep = SCREEN_DISTANCE / $rz * $this->size;
    
            // 画面の中心が (0,0) から、左上が (0,0) の座標軸に変換
            $xp = SCREEN_WIDTH / 2 + $xp;
            $yp = SCREEN_HEIGHT / 2 - $yp;
    
            return new Vec3($xp, $yp, $sizep);    
        } else {
            return null;
        }
    }

Draw の方はいたってシンプルに Projection の結果が背面にまわったせいで null となっていない限り

x,y の位置に縦と横が z の大きさの四角を一つ描きます。

     public function Draw(Scene $scene, Node $node): void
    {
        $xysize = $this->Projection($scene, $node);
        if (is_null($xysize)) {
            // do nothing
        } else {
            $rect = new SDL_Rect((int)$xysize->x, (int)$xysize->y, (int)$xysize->z, (int)$xysize->z); 
            SDL_RenderDrawRect($scene->renderer, $rect);    
        }
    }
}

シーンのデータは、スクリーンの高さの8割の半径で、3000 点で出来た球体を２個置きました。

// シーン上のデータを作成する
function Buildup(Scene $scene)
{
    // 点群で球面
    $sphereRadius = SCREEN_HEIGHT * 0.8;
    $numDots = 3000;
    $size = 8;
    for ($i = 0; $i < $numDots; $i++) {
        // y 軸の先からの傾きθ 0 から 2pi
        $theta = (float)mt_rand(0,1000) / 1000.0 * 2.0 * pi();  
        // xz 平面での x 軸 からの傾きφ 0 から 2pi
        $phi = (float)mt_rand(0,1000) / 1000.0 * 2.0 * pi();
        // 点を追加していく
        $sphere[] = new PolarDot($sphereRadius, $theta, $phi, $size);
    }
    // 全部の点を１個の node として位置を決めて２個追加
    $scene->nodes[] = new Node($sphere, new Vec3(0,0,1000));
    $scene->nodes[] = new Node($sphere, new Vec3(0,0,2000));
}

Update() での描画本体もほぼ同じですが、地球の自転のようなアニメーションをさせるために Geometory が PolarDot クラスの場合だけ Draw の前に経度にあたる phi をフレーム毎に 0.01 ラジアン回転させるように変更しました。

        foreach($node->geometries as $geometry) {
            if (get_class($geometry) === 'PolarDot') {
                $geometry->phi += 0.01;
            }
            $geometry->Draw($scene, $node);
        }

長くなりましたが変更点は以上です！ 実行したものがこちらになります。

まとめ

３回シリーズで PHP と SDL を使ったグラフィクスについてお届けしました！！

テーマを絞り込むために autoload に合ったファイル分割、composer によるプロジェクト作成、phpunit でのテストなど通常の PHP での開発に使うものは全て省略しましたが、それらはまた別の機会に触れたいと思います。

PHP をつかったシンプルなオブジェクト指向と SDL を使ったグラフィクスの組み合わせはとても楽しく、また当初想像していたのより高速に動作してくれて、近年の PHP の性能の高さの片鱗を垣間見ることが出来た体験でした！

弊社では PHP で面白いことに挑戦してくれる方の応募を絶賛お待ちしております！ ⇒ 採用情報

arrow_back 前の記事へ
一覧へ戻る
次の記事へ arrow_forward

ブログ記事検索

このブログについて

このブログは、札幌市・仙台市の「株式会社インフィニットループ」が運営する技術ブログです。 お仕事で使えるITネタを社員たちが発信します！

最新の記事

人気タグ

YouTube あいえるちゃんねる
広報ブログ